Using Mathematica's DSolve function on Example used for Finite Differencing Examples

Mathematica's DSolve function finds closed-form expressions for solutions to differential equations, when possible. There is a related function called NDSolve that finds numerical solutions that can be used when DSolve gives up. Here are some examples of using DSolve:

Note that the solution is given as a rule, just like for the function Solve. Because no initial condition was specified, the solution involves an unknown constant, C[1].   In the next  case an initial condition was specified for the differential equation, so there is no undetermined constant in the solution.

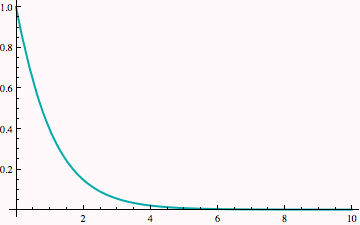
The next statement extracts y (x) for plotting ...

Created by Wolfram Mathematica 6.0  (06 November 2007)