Fourier Series: Example using Derived Functions

Define a function to use as an example:

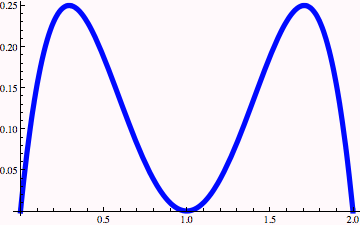
Now calculate Fourier amplitudes for this function…

The odd terms should all vanish because the function is even around the center x=

Make the Fourier series representation by taking the dot product of the AmplitudeVectors with the BasisVectors:

For myfunction we write the Fourier series out to six terms as:

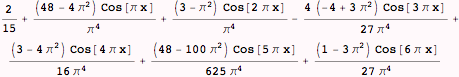
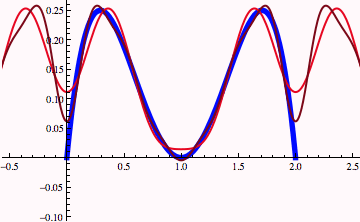
Note the periodicity of the plot above.  The wavelength is 2. Only three terms were calculated in the Fourier series representation of myfunction. Below the Fourier series and the exact function are shown superposed.

Now the calculation is repeated but retaining 6 terms in the Fourier series representation and hopefully obtaining a more accurate representation of myfunction.

Created by Wolfram Mathematica 6.0  (24 October 2007)