Surface Integration

Example: Integrating an Orientation-Dependent Surface Tension over the surface of a cube and a sphere

Vector function for surface of sphere of radius R, u is longitude (u ∈ (0, 2π)) and v is latitude (v ∈ (-, ))
(Note: this is the parametric form of the equation of the sphere )

In[52]:=

The coordinate vectors at (u,v) (Note: these vectors are tangent to the sphere surface at the point (u,v).)

In[53]:=

Out[53]=

Out[54]=

A normal vector and its unit normal: no surprise here, the unit normal is just the vector from the origin to a point on a unit sphere...

In[55]:=

Out[56]=

Out[57]=

Out[58]=

Now, suppose the surface energy ( ) depends on the local orientation of the surface. This is case for many single crystals. If the single crystal is cubic, it is often the case that the (100) planes have lower energy than the (111) planes.  The following model for orientation-dependent surface tension has this behavior and can be employed for illustrative purposes:

In[59]:=

Here is a plot of our model aniostropic surface energy-- the lobes at [111] indicate that those orientations have higher energy:

In[60]:=

Out[60]=

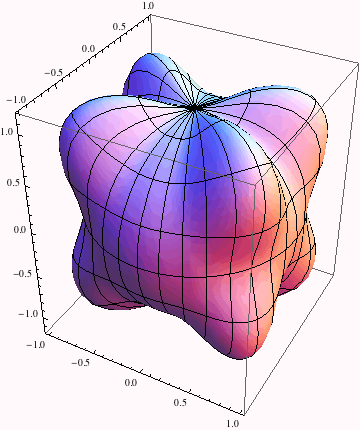
The total energy of a spherical particle of unit radius having the anisotropic surface tension represented above is given by the double integral

In[61]:=

Out[61]=

Compare to Cube of same volume as the unit sphere: =

In[62]:=

Out[62]=

In[63]:=

Out[63]=

In[64]:=

Out[64]=

If the anisotropy factor is greater than about 25, then a cube is much lower energy

In[65]:=

Out[65]=

This computation compared two fixed shapes of the same volume.  To find which shape of all the possible shapes, one would use a procedure known as the Wulff construction.

Created by Wolfram Mathematica 6.0  (28 September 2007)