Using Green's theorem to Reduce a Surface Integration to a Path Integral

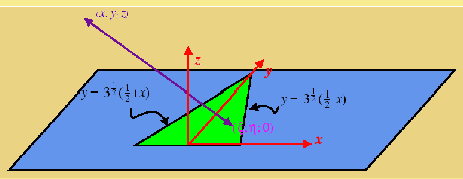
  Suppose there is a uniformly charged surface  (σ≡charge/area=1) occupying an equilaterial triangle in the z=0 plane:
    

The electrical potential goes like , therefore the potential of a unit charge located at (x,y,z) from a small surface patch at (ξ,η,0) is =

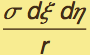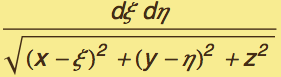
Try to convert the integral over the region to an integral over its boundary.  We may be able to find a closed form—and even if not the numerical integration should be much more efficient...

We will use Green's Theorem in the Plane:
∫∫(-)dxdy = ∫(dx +dy)

Find a function, that when we take the derivative with respect to x, we get 1/r.
We will let be the function we find, and set =0

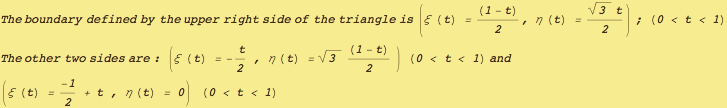
To use Green's theorem in the plane   =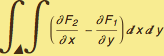
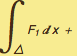
Try to find a vector function (, ) that matches the integrand over the domain.  Let = 0, then to find which when differentiated by η gives 1/r

In[6]:=

Out[6]=

The third (horizontal) boundary of the triangle patch looks like the easiest, let's see if an integral can be found over that patch:

In[7]:=

Out[7]=

The following attempt to find a closed-form integral seems to take "forever" to evaluate and I ended up aborting it, then continuing to evaluate the remainder of the notebook. This command has been commented out to avoid evaluation

In[8]:=

In[9]:=

Out[9]=

In[10]:=

Out[10]=

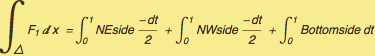
In[11]:=

Out[11]=

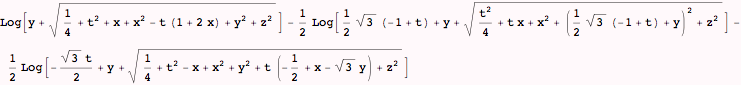
The following attempt to find a closed-form integral seems to take "forever" to evaluate and I ended up aborting it, then continuing to evaluate the remainder of the notebook. This command has been commented out to avoid evaluation

In[12]:=

Created by Wolfram Mathematica 6.0  (28 September 2007)