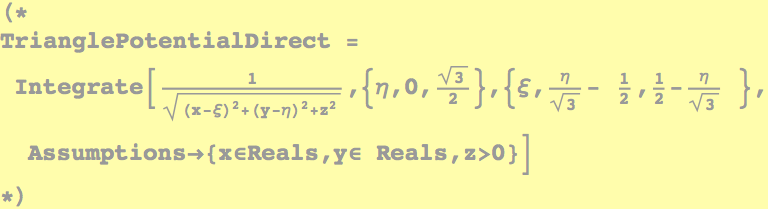
Multidimensional Integrals: Example Potential over a Triangular Charged Patch

We will try to find the potential due to a triangular patch on a particle located at (x,y,z=1) (Warning, this will take a long time to evaluate, users will probably need to abort the evaluation, the code is commented out to prevent this...)

Trying to do this directly either takes too long or there is no closed form! We have to work around it by using Indefinite Integrals

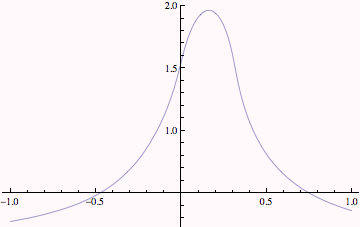
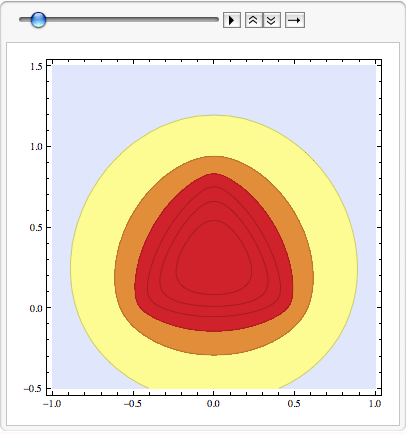
We will create contourplots (level sets of constant potential) at as a function of different heights. We check the timing of the computation---it will be compared to a more efficient method in the next lecture.

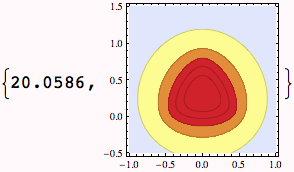
then compute them for subsequent animation. (warning, this will take quite a while to evaluate on most machines, a "progress monitor" has been added.)

Created by Wolfram Mathematica 6.0  (24 September 2007)