Path-Independent Integrals on a Limited Subspace: Vector Fields with Non-Vanishing Curl Except on a Particular Surface

For a last example, suppose the curl vanishes on the cylindrical surface defined above:

Suppose we can find a function that has a non-vanishing curl on this surface

We want to find a function which is generally non-curl free, but for which the curl vanishes on a surface. Let's pick the cylinder as our surface.

If  a function can be found, that has the following curl, then we will have constructed such a function,

It is easy to see that this is the curl of Stooge, where we construct Stooge by integrating.

In fact, we could add to Stooge, any vector function that has vanishing curl--there are an infinite number of these

Its integral doesn't care which path around the cylinder it takes, the integrand doesn't depend on P(t)

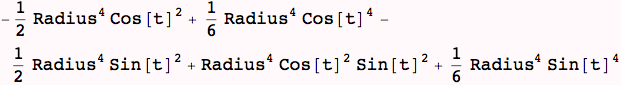
This is the value for *any* path on the cylinder that is closed.

Created by Wolfram Mathematica 6.0  (24 September 2007)