Examples of Path-Dependent Integrals:  Vector Fields with Non-Vanishing Curl

Here is a vector function (xyz, xyz, xyz) for which the curl does not vanish anywhere, except the origin

These are the conditions that the curl is zero:

There is only one point where this occurs:

Let's evaluate the integral of the vector potential (   ) for any  curve that wraps around a cylinder of radius R with an axis that coincides with the z-axis

Any curve that wraps around the cylinder can be parameritized as (x(t), y(t), z(t)) = (R cos(t), R sin(t), A (t)) where (t) = (t + 2π) and in particular (0) = (2π).
Therefore d=    (-R sin(t), R cos(t), (t)) dt = (-y(t), x(t), A (t))     dt
The integrand for an integral of "VectorFunction" around such a curve is (written in terms of an arbitrary P(t):

The integral depends on the choice of P(t)

Let's introduce some specific periodic functions for P. Note how the value of the integral changes as the path changes:

However, here is  curious result which shows that some special paths can ``accidentally'' have zero integrals : let P(t) = cos(n t),

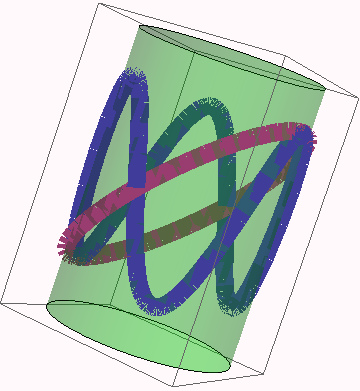
Apparently, the symmetry of the vector function causes cancelation (note results for P = Sin and P=Cos, differ by a minus sign)
But, why doesn't n=1 give us the correct result above? Note that the denominator goes to zero as n→1

Created by Wolfram Mathematica 6.0  (24 September 2007)