A Visualization Example of the Curl

There is a very useful free software tool for solving minimal surface (and many other) variational problems called Surface Evolver by Ken Brakke.  To use Surface Evolver to greatest possible advantage, a user should be adept at using results from vector analysis.  Mathematica's Vector Analysis package is very helpful aid for developing powerful Evolver codes.  The following example is extracted from the Surface Evolver manual.

Visualize the vector field for n=3, note that the function will be singular near the z-axis

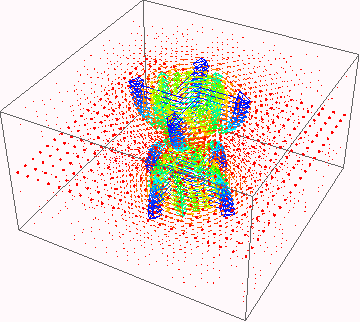
using the symmetry of the field

Calculate the curl of the function using the VectorAnalysis package--note that the coordinate system is specified as cartesian.
For the particular case of n=3:

Define a new vector function for the curl for general n

Demonstrate the assertion that the curl has a fairly simple form and is sphericaly symmetric for n=1

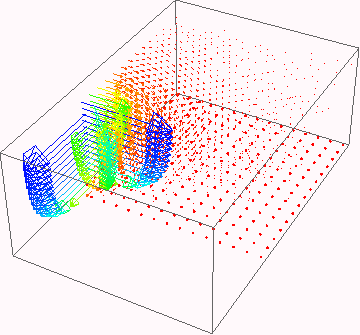
Visualize the curl for n=1, it will be necessary to "zoom" in to see the field.

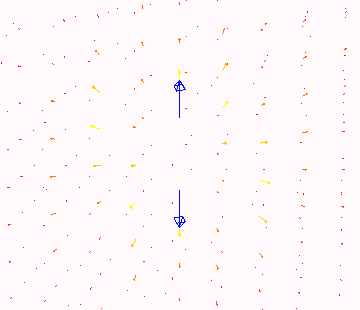
Demonstrate that the divergence of the curl vanishes for the above function independent of n

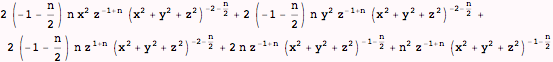
Created by Wolfram Mathematica 6.0  (21 September 2007)