Arc Length and Re-parameterizing Curves

Make up two functions that will illustrate the difference between a curve's parameter and its arclength

Here is a general way to take a function of a general parameter, t, and compute the arc length traversed as t varies from one value to another:

This is the arclength up to the parameter t, the integral does not have a closed-form

Applying this to the function Bendy defined above:

This is the arclength up to the parameter t, the integral does have a closed-form, but is not easily invertible.

The arc length in this case is given by a tabulated  function called an elliptic integral and after checking its behavior at t = 0 we can plot it over the range {t,0,2π}:

However, the inverse exits, we can find a t(s) (the curve parameter t for any arclength s)

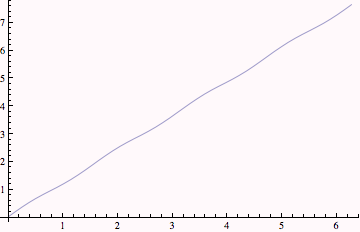
Alternatively, we can evaluate the expression for arc length numerically using the following:

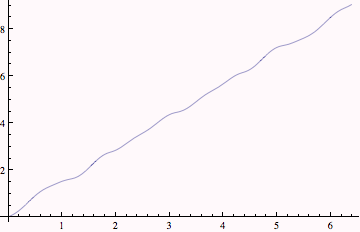
Created by Wolfram Mathematica 6.0  (20 September 2007)