The Time-Dependent Solution to the Diffusion Equation in the Plane Rectangular Initial Conditions

This is the solution to the time-dependent diffusion equation in the infinite plane for iniital conditions c = 1 inside a rectangle (-a/2 < x < a/2 && -b/2 < y < b/2) and zero outside.

Introduce a fixed model parameter and non-dimensional variables:

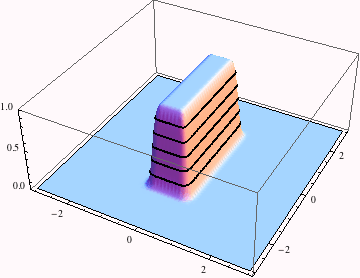
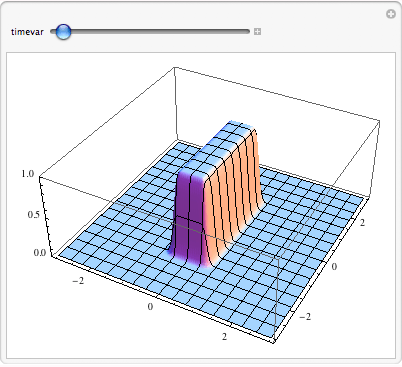
Visualize the solution by plotting the concentration as  function of x and y, and animate as  function of time.

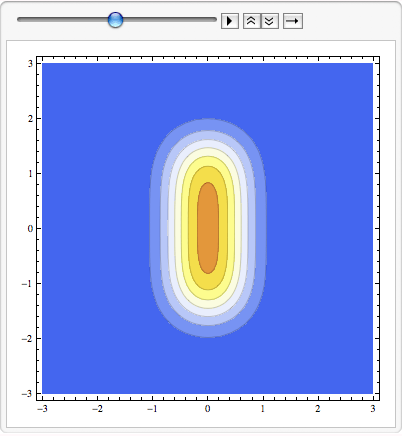
Another visualization scheme: plot the isoconcentration lines as  function of x and y, and animate as function of time.  This is like the temporal evolution of a topographical map.

Created by Wolfram Mathematica 6.0  (17 September 2007)