Visualizing Local Tangent Vectors of Space Curves

Compute the local derivative of the vector that we visualized above: =

Write out a function for the derivative:

Plot it.... Note that it doesn't "appear" to be periodic, which would be wrong.

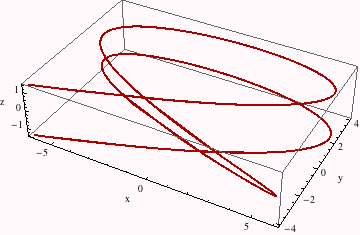
The puzzle can be visualizing the time-development of both curves:

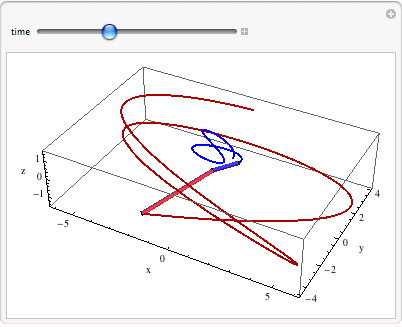
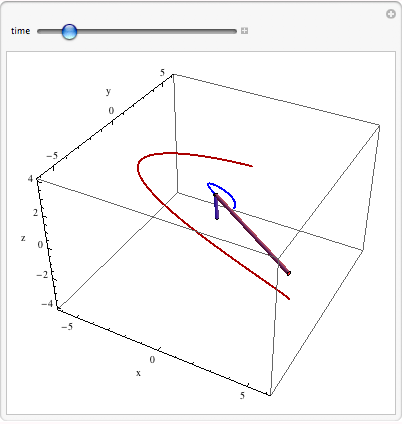
To visualize the "tangency property,"  we translate the derivative-vector to the end of the space curve

Created by Wolfram Mathematica 6.0  (17 September 2007)