Two-Dimensional Stress under Rotation: Mohr's Circle

The above three equations can be graphically represented  as Mohr's circle of stress (see accompanying class notes). The equations show the way in which the stress tensor components in a two-dimensional state of stress (a "biaxial" stress state) vary with orientation of the coordinate system in which the stresses are described.

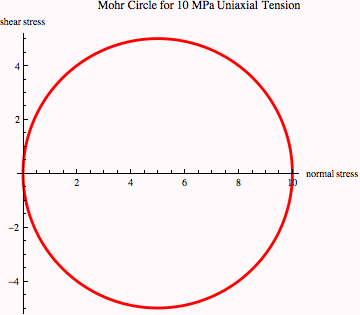
Example of Mohr's circle for two-dimensional body in uniaxial tension with = 10 MPa and all other stress components equal to zero

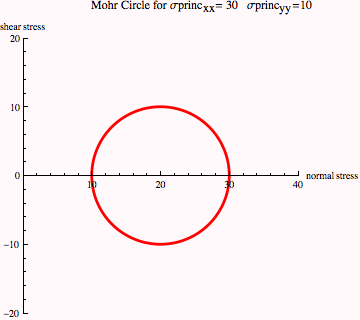
Comparing this plot with Figure 10-3 in the lecture notes, we see that the maximum and minimum tensile stresses are 10 and 30 MPa (from intercepts with x axis), as expected, and the maximum shear stress is ±5 MPa and it is experienced on a plane oriented at 2θ = 90° or θ = 45° to the tensile axis (remember that angles on Mohr's circle plots are twice the angle in the body).

Created by Wolfram Mathematica 6.0  (12 September 2007)