General Stress State Rotated from the Principal Axes  System

This is a general state, we will rotate about the z-axis and compare the result to a general two-dimensional stress state.

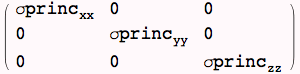
Rotation about z-axis by angle θ

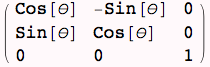
Transformation to general two-dimensional stress state coordinate system by rotating the principal system by θ around z-axis

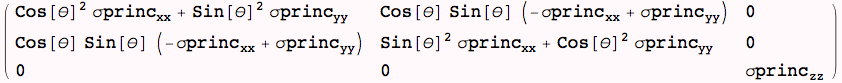
Writing the same equation in a slightly different way...

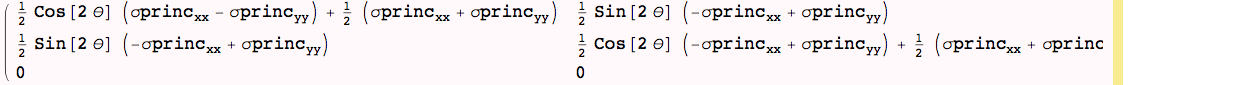
Naming the coefficients of the rotated two-dimensional state:

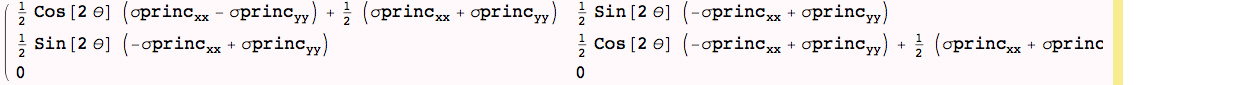
Looking at the x-y components of stress (i.e, the upper-left  2×2 submatrix), notice that there are two invariants of the generalized two-dimensional  stress state: The trace and the determinant:

Do not depend on θ; thus illustrating the invariance of these quantities under rotation of coordinate rotations.

Created by Wolfram Mathematica 6.0  (12 September 2007)