Coordinate Transformations; The Eigenbasis

Shows that the transformation to the diagonal basis is a rotation of π/4

Which makes sense considering in initialization steps that mymatrix was created with a rotation on π/4 of a diagonal matrix

The next command produces an orthonormal basis of the eigenspace (i.e., the eigenvectors are of unit magnitude):

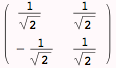
The command RotationTransform computes a matrix that will rotate vectors ccw about the origin in two dimensions, by a specified angle:

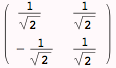
This last result shows that the transformation to the eigenvector space involves rotation by π/4--and that the matrix corresponding to the eigenvectors produces this same transformation

Here is a demonstration of the general result A = , where is an eigenvector and λ its corresponding eigenvalue:

MatrixPower multiplies a matrix by itself n times…

Created by Wolfram Mathematica 6.0  (12 September 2007)