Background

The positive square root of -1

Complex numbers are composed of a real part + an imaginary part

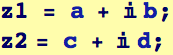
Simple operations on complex numbers

Mathematica does not assume that symbols are necessarily real...

However, the Mathematica function ComplexExpand does assume that the variables are real....

Function to convert to Polar Form

Note: the function Arg[z] returns an angle in the range -π to π which measures the inclination of z with respect to the +Re axis in the complex plane.

Created by Wolfram Mathematica 6.0  (07 September 2007)