Solving Systems of Equations

Consider the set of equations
     x + 2y +  z  +  t  = a
    -x + 4y - 2z         = b
     x + 3y + 4z + 5t = c
     x          +  z  +   t = d
We illustrate how to use a matrix representation to write these out and solve them…     

Start with the matrix of coefficients of the variables, mymatrix:

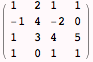
The system of equations will only have a unique solution if the determinant of mymatrix is nonzero.

The left-hand side of the first equation will be

and the left-hand side of all four equations will be

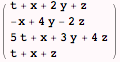
Now define an indexed variable linsys with four entries, each being one of the equations in the system of interest:

Solving the set of equations for the unknowns

Created by Wolfram Mathematica 6.0  (06 September 2007)