Using Recursion to Program

Functions that call themselves...

The canonical programming example is the factorial function n! = (n)×(n-1) ×(n-2)×…×(1) where 0! ≡  1; here is a reasonably clever way to use the fact that (n+1)! = (n+1)×n!

try it out...

Ooops, This isn't what was expected, but upon reflection it is correct--we forgot to define a part of the rule. (Note also that the message window produced an error about recursion limits) Add the second part of the definition. Here, we don't use delayed evaluation (:=) because we want to assign a value immediately.

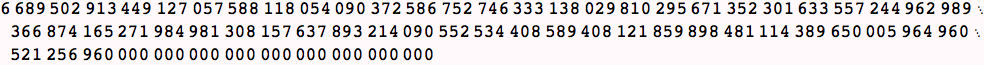
Here is where the recursion limit comes in : our function keeps on calling itself (i.e., recursively). Unless a limit is set the program would keep running forever. Mathematica builds in a limit to how many times a function will call itself:

Speed versus Memory in Functions

Using immediate assignment in a function: spending memory to buy time: Each time the function is called, it makes an extra assignment so that previous values can be recalled if needed.

This version takes a bit longer the first time, because we are storing data in memory ...

But, the next time it is called, the result is much faster.

Created by Wolfram Mathematica 6.0  (06 September 2007)