
Resonance Phenomena
Resonance phenomena simulated by finite differences and biased noise inputs
In Lecture-21.nb, a second-order differencing scheme that iteratively solved y'' + βy' + γy=0 with the specification of two initial values.
Modify this to add a little random noise to y[i] at each step and observe how this behaves---this version will store the noise added at each iteration so that it can be visualized later....
Setting up a function that takes particular parameters and a "noise amplitude" of ![]()
![]()
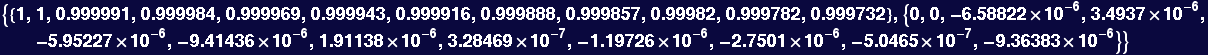
![]()
![]()
![[Graphics:HTMLFiles/Lecture-23_8.gif]](HTMLFiles/Lecture-23_8.gif)
![]()
![[Graphics:HTMLFiles/Lecture-23_11.gif]](HTMLFiles/Lecture-23_11.gif)
![]()
Now suppose there is a periodic bias that tends to kick the displacement one direction more than the other:

![]()
Generate the data set---this takes quite a while
![]()
![[Graphics:HTMLFiles/Lecture-23_18.gif]](HTMLFiles/Lecture-23_18.gif)
![]()
![[Graphics:HTMLFiles/Lecture-23_20.gif]](HTMLFiles/Lecture-23_20.gif)
![]()
Resonance Phenomena by Solution of the ODE
The "periodic forcing function" can be any periodic function (i.e., a fourier series), but it is a bit simpler to analyze the effect of each mode separately. Below, the forcing function will be assumed to be ![]() cos(
cos(![]() t)
t)
Solve problems in terms of the mass and natural frequency--eliminate the spring constant in equations by defining it in terms of the mass and natural frequency.
![]()
![]()
Mathematica can solve the nonhomogeneous ODE with a forcing function at with an applied frequency:
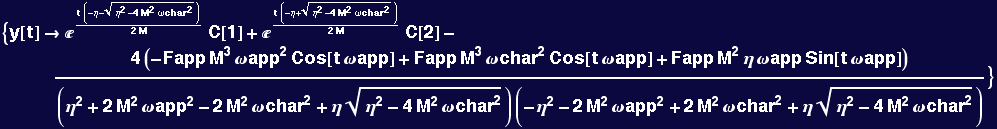
The general solution of the heterogeneous ODE is the sum of the homogeneous solution (i.e., the one for which the right-hand-side is zero) and the particular solution (i.e., the one for the particular right-hand-side of the ODE)
![]()
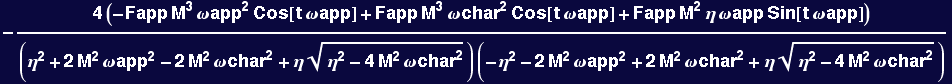
![]()
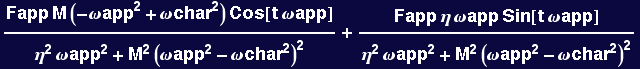
The particular solutions only picks up modes from the forcing term
The homogeneous solution only has he natural frequencies
![]()
![]()
The General Solution is the combination of two different frequencies--this should give rise to beats if the driving frequency differs from the natural frequency
![]()
The following shows that the solution is unphysical when ωapp → ωchar AND η→0
![]()
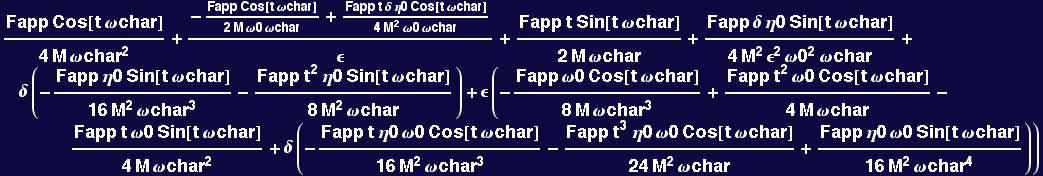
We can determine the behavir near the singularity by looking at the effect of each term above:
1. If the forcing frequency approaches the resonance frequency (ε→0), the solution is unbounded because there is no δ in the first part of the second term's numerator
2. If the viscosity approaches zero (δ→0), the solution will have a linearly growing applitude because of the third term
3. Other cases will depend on how the ratio δ/ε scales.
The following demonstrates the zero viscosity case, needs to be analyzed carefully (as above) otherwise one might miss terms:
![]()
![(Fapp (-ωapp^2 + ωchar^2) Cos[t ωapp])/(M (ωapp^2 - ωchar^2)^2)](HTMLFiles/Lecture-23_39.gif)
Create a Mathematica function that returns the solution for specified mass, viscous term, characteristic and applied frequencies
Experiment by plotting for many different values:
Undamped Resonance:
![[Graphics:HTMLFiles/Lecture-23_42.gif]](HTMLFiles/Lecture-23_42.gif)
![]()
Undamped Near Resonance:
![[Graphics:HTMLFiles/Lecture-23_45.gif]](HTMLFiles/Lecture-23_45.gif)
![]()
Damped Resonance:
![[Graphics:HTMLFiles/Lecture-23_48.gif]](HTMLFiles/Lecture-23_48.gif)
![]()
Overdamped Resonance:
![[Graphics:HTMLFiles/Lecture-23_51.gif]](HTMLFiles/Lecture-23_51.gif)
![]()
Damped Near Resonance:
![[Graphics:HTMLFiles/Lecture-23_54.gif]](HTMLFiles/Lecture-23_54.gif)
![]()
Heavily damped Near Resonance:
![]()
![[Graphics:HTMLFiles/Lecture-23_57.gif]](HTMLFiles/Lecture-23_57.gif)
![]()
| Created by Mathematica (December 18, 2005) |