Periodic Phenomena
Let's begin by "looking" at a familiar periodic phenomena:
In[81]:=
![[Graphics:HTMLFiles/Lecture-17_17.gif]](HTMLFiles/Lecture-17_17.gif)
Out[96]=
![]()
In[97]:=
![]()
![[Graphics:HTMLFiles/Lecture-17_20.gif]](HTMLFiles/Lecture-17_20.gif)
Out[97]=
![]()
Let's see if we can play this: l![[Graphics:HTMLFiles/Lecture-17_22.gif]](HTMLFiles/Lecture-17_22.gif)
In[98]:=
![]()
In[99]:=
![]()
Out[99]=
![]()
In[102]:=
![]()
![[Graphics:HTMLFiles/Lecture-17_27.gif]](HTMLFiles/Lecture-17_27.gif)
Out[102]=
![]()
In[110]:=
![]()
![[Graphics:HTMLFiles/Lecture-17_30.gif]](HTMLFiles/Lecture-17_30.gif)
![]()
![]()
Out[110]=
![]()
Fourier Series
Define a function that is periodic with wavelength λ using the modulus function:
Boomerang uses Mod to force a function, f, with a single argument, x, to be periodic with wavelength λ
![]()
![]()
![]()
The following step uses Boomerang to produce a periodic repetition of AFunction over the range 0 < x < 6:
![]()
![]()
![[Graphics:HTMLFiles/Lecture-17_39.gif]](HTMLFiles/Lecture-17_39.gif)
![]()
Demonstration of the orthogonality of the trigonometric functions
![]()
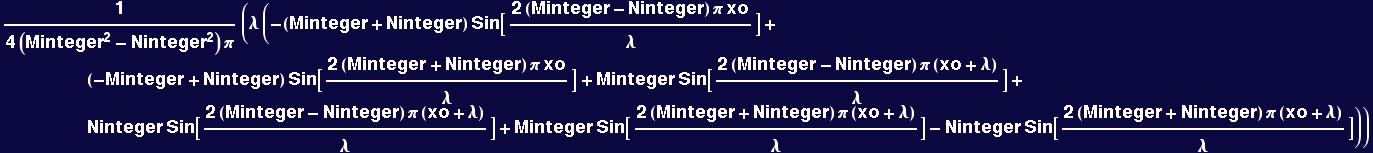
![]()
![]()
![]()
![]()
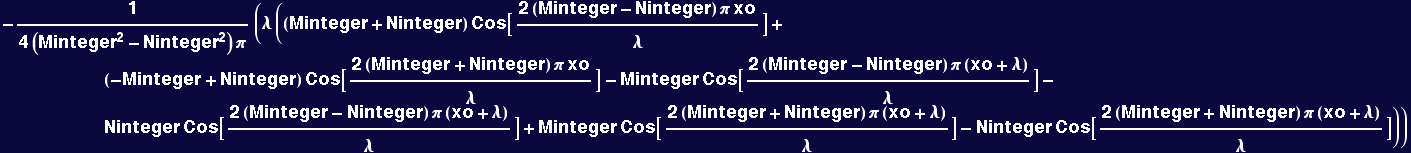
![]()
![]()
![]()
![]()
![]()
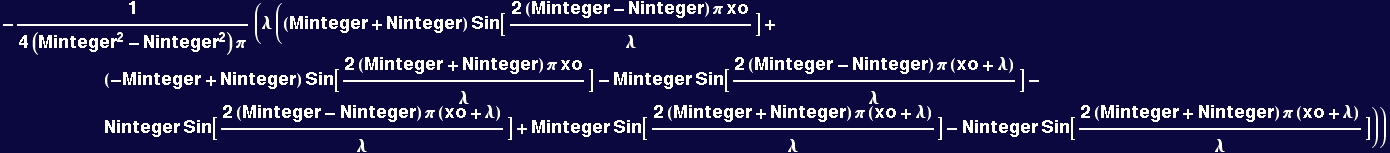
![]()
![]()
![]()
![]()
Example of determination of fourier coefficients
First we will "do it the hard way" and write short programs that evaluate Fourier coefficients; then we will demonstrate how to make use of built-in functions in Mathematica's FourierTransform package…
Define functions based on the formulas derived for the fourier amplitudes
The constant term:
![]()
A function that defines each even amplitude individually (this is not very efficient, it would be better to evaluate the integral once and use that result)
Define the zeroth odd term as zero for symmetry with the even terms:
![]()
A function to create a vector of amplitudes for the odd terms and one for the even terms
![]()
![]()
Define a function to use as an example:
![]()
![]()
![[Graphics:HTMLFiles/Lecture-17_67.gif]](HTMLFiles/Lecture-17_67.gif)
![]()
Now calculate Fourier amplitudes for this function…
![]()
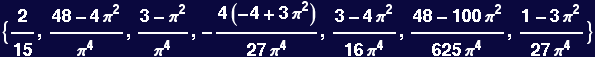
The odd terms should all vanish because the function is even around the center x=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Make the Fourier series representation by taking the dot product of the AmplitudeVectors with the BasisVectors:
For myfunction we write the Fourier series out to six terms as:
![]()
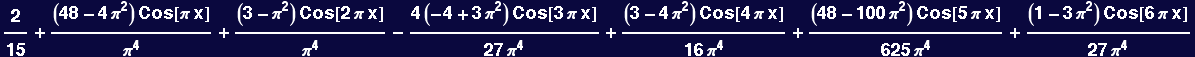
![]()
![[Graphics:HTMLFiles/Lecture-17_84.gif]](HTMLFiles/Lecture-17_84.gif)
![]()
Note the periodicity of the plot above. The wavelength is 2. Only three terms were calculated in the Fourier series representation of myfunction. Below the Fourier series and the exact function are shown superposed.
![]()
![[Graphics:HTMLFiles/Lecture-17_87.gif]](HTMLFiles/Lecture-17_87.gif)
![]()
Now the calculation is repeated but retaining 6 terms in the Fourier series representation and hopefully obtaining a more accurate representation of myfunction.
![[Graphics:HTMLFiles/Lecture-17_90.gif]](HTMLFiles/Lecture-17_90.gif)
![]()
![]()
![[Graphics:HTMLFiles/Lecture-17_93.gif]](HTMLFiles/Lecture-17_93.gif)
![]()
Fourier Series Coefficients using Mathematica's package:
![]()
![]()
![[Graphics:HTMLFiles/Lecture-17_98.gif]](HTMLFiles/Lecture-17_98.gif)
![]()
Mathematica's Fourier Series functions are defined for function that are periodic in the domain x ∈ (-1/2,1/2). So we need to map the periodic functions to this domain
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-17_104.gif]](HTMLFiles/Lecture-17_104.gif)
![]()
![]()
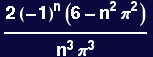
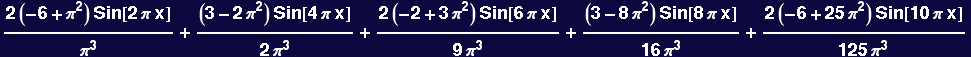
![]()
The function above will work, but it is horribly inefficient! Because it asks FourierTrigSeries to calculate one more term each time, it is doing some redundant work. We can fix this up by having
it calculate one new term and adding to the sum calculated previously. Here it is:
![]()
The following will demonstrate how convergence is difficult where the function changes rapidly---this is known as Gibbs' Phenomenon
Recall the definition used above for myfunction
![]()
![]()
Reduce myfunction to a domain so that we can use Mathematica's Fourier Package on it.
![]()
![]()
General form of the even amplitudes
![]()
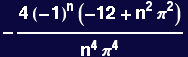
![]()
![]()
Illustrate how amplitude of each term behaves. This plot indicates that the short wavelength contributions are smaller and smaller.
![[Graphics:HTMLFiles/Lecture-17_186.gif]](HTMLFiles/Lecture-17_186.gif)
![]()
![]()
![[Graphics:HTMLFiles/Lecture-17_189.gif]](HTMLFiles/Lecture-17_189.gif)
![]()
| Created by Mathematica (November 2, 2005) |