Lecture-16.nb

Generalizations of the Fundamental Theorem of Calculus (Part II)

Using Divergence theorem to find London attraction potential between point particle and a finite cylinder.

Find such that div is -1/(Overscript[r, →] - Overscript[x, →])^6 where = (ξ,η,ζ) is a position in the cylinder and =(x,y,z) is a general position in space (A fairly general method to do this and similar problems can be found in Argento C; Jagota A; Carter WC ``Surface formulation for molecular interactions of macroscopic bodies'' J.Mech. Physics Solids 1997, pp 1161-1183 .

The following is a ``guess'' at the vector potential; it will be verified as the correct one by checking its divergence.

In[1]:=

$FVecLondon = 1/(3 ((ξ - x)^2 + (η - y)^2 + (ζ - z)^2)^3) {ξ - x, η - y, ζ - z}$

Out[1]=

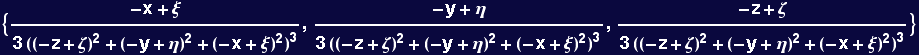
In[2]:=

The following verifies that the correct vector potential is obtained

In[3]:=

Out[3]=

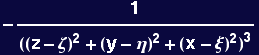
-1/((z - ζ)^2 + (y - η)^2 + (x - ξ)^2)^3

Therefore, ∫_ (CylinderVolume) 1/(Overscript[r, →] - Overscript[x, →])^6 dV = ∫_ (CylinderSurfaces) •d = ∫_ (CylinderSurface) •d+ ∫_ (CylinderEnds) •d is the total interaction between a point an a cylinder.

Cylindrical coordinates: (ξ,η,ζ) = (r Cos[t], r Sin[t], ζ):
One cylindrical surface r= R = const. t ∈ (0, 2π), ζ ∈ (- , )
Two caps r ∈ (0,R) t ∈ (0, 2π), ζ=±

Cylinder Surface normals and differential quantities

The following is a parametric representation of a cylinder surface that is coaxial with the z-axis (the cylinder ends will be included later)

In[4]:=

Out[4]=

The infinitessimal surface vectors and for the cylinder surface are obtained by differentiation; they will be used to find the surface patch d.

In[5]:=

Out[5]=

$General :: spell1 : Possible spelling error: new symbol name \"CylSurfRz\" is similar to existing symbol \"CylSurfRt\". More…$

Out[6]=

The surface normal given by × for the cylinder surface, there for the following (multiplied by dθ dz) is the infinitessimal oriented surface patch d.

In[7]:=

Out[7]=

The integrand to be evaluated over the cylinder surface is the vector potential, dotted into

In[8]:=

Out[8]=

(R (R - x Cos[t] - y Sin[t]))/(3 (R^2 + x^2 + y^2 + (z - ζ)^2 - 2 R (x Cos[t] + y Sin[t]))^3)

Closed form for integral is un-findable, use a numeric integration--this will be written in two forms
1) A general function of x,y,z of the point particle and the cylinder radius and length.
2) Because of the polar symmetry, the integral should be a function of only r =

We can use the same function name twice, but with a different number of arguments. But, first we will try to do at least one of the two integrations symbolically. If we can do this, it will reduce the original numerical integration from three dimensions down to 1---which is a nice bargain if we can find it.

Try and see if we can do one of the two integrals. First, let's try theta:

In[9]:=

Out[9]=

The integral over theta gives no symbolic form...Try and see if we can do one of the two integrals. So, let's try ζ:

In[10]:=

Out[10]=

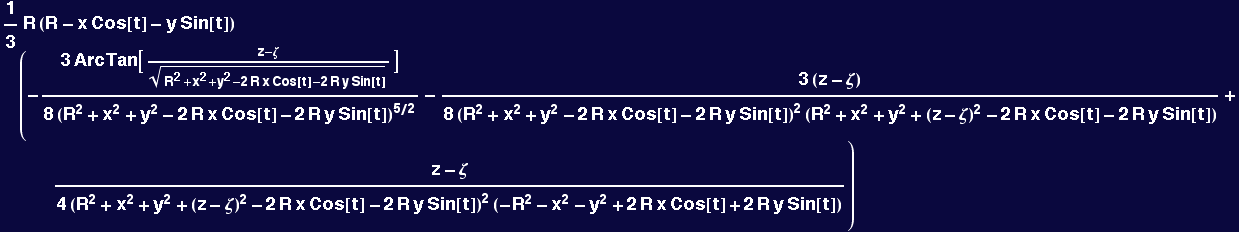
Here we will use a trickof using Evaluate[] in a function definition to save time--a small diversion here will demonstrate why this is efficient

In[17]:=

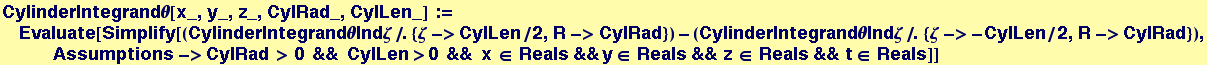
In[18]:=

$CylinderContribution[x_, y_, z_, CylRad_ , CylLen_] := NIntegrate[Evaluate[CylinderIntegrandθ[x, y, z, CylRad, CylLen], {t, 0, 2π}]]$

Because of the polar symmetry, this contribution should only be a function of the distance ((x^2 + y^2)^(1/2)), so we can write a new function (with the same name) with fewer arguments

In[19]:=

$CylinderContribution[dist_, z_, CylRad_ , CylLen_] := NIntegrate[Evaluate[CylinderIntegrandθ[dist, 0, z, CylRad, CylLen], {t, 0, 2π}]]$

Checking the numerical integration for the first form of the function

In[20]:=

Out[20]=

Checking the numerical integration for the second form of the function

In[21]:=

Out[21]=

Top Cap Surface normals and differential quantities, parallel method to cylinder surface

In[22]:=

TopSurf = {r Cos[t], r Sin[t], L/2}

Out[22]=

{r Cos[t], r Sin[t], L/2}

In[23]:=

Out[23]=

$General :: spell1 : Possible spelling error: new symbol name \"TopSurfRr\" is similar to existing symbol \"TopSurfRt\". More…$

Out[24]=

In[25]:=

Out[25]=

In[26]:=

Out[26]=

(r (L - 2 z))/(6 (1/4 (L - 2 z)^2 + (x - r Cos[t])^2 + (y - r Sin[t])^2)^3)

Because we will need to numerically integrate over r and over t, we might try the same trick as above and see if one of these integrals can be expressed in closed form.

Integrating over θ doesn't provide a closed form (this next step takes a while to evaluate...)

In[27]:=

$General :: spell1 : Possible spelling error: new symbol name \"TopIntegrandζr\" is similar to existing symbol \"TopIntegrandθr\". More…$

$Integrate[(r (L - 2 z))/(6 (1/4 (L - 2 z)^2 + (x - r Cos[t])^2 + (y - r Sin[t])^2)^3), {t, 0, 2 π}, Assumptions→ {r>0, L>0, x∈Reals, y∈Reals, z∈Reals}]$

Out[27]=

Integrating over r does work

In[28]:=

Out[28]=

In[29]:=

$TopIntegrandθ[x_, y_, z_, CylRad_, CylLen_] := Evaluate[Simplify[(TopIntegrandθIndr/.{r->CylRad, L->CylLen}) - (TopIntegrandθIndr/.{r->0, L->CylLen})]]$

$General :: spell1 : Possible spelling error: new symbol name \"TopIntegrandθ\" is similar to existing symbol \"TopIntegrandθr\". More…$

In[30]:=

$TopContribution[xpos_, ypos_, zpos_, CylRad_ , CylLen_] := NIntegrate[Evaluate[TopIntegrandθ[xpos, ypos, zpos, CylRad, CylLen], {t, 0, 2 π}]]$

In[31]:=

$TopContribution[dist_, zpos_, CylRad_ , CylLen_] := NIntegrate[Evaluate[TopIntegrandθ[dist, 0, zpos, CylRad, CylLen], {t, 0, 2 π}]]$

In[32]:=

Out[32]=

In[33]:=

Out[33]=

Bottom Cap Surface normals and differential quantities

In[34]:=

BotSurf = {r Cos[t], r Sin[t], -L/2}

Out[34]=

{r Cos[t], r Sin[t], -L/2}

In[35]:=

Out[35]=

$General :: spell1 : Possible spelling error: new symbol name \"BotSurfRr\" is similar to existing symbol \"BotSurfRt\". More…$

Out[36]=

In[37]:=

Out[37]=

In[38]:=

Out[38]=

(32 r (L + 2 z))/(3 (4 (r^2 + x^2 + y^2) + (L + 2 z)^2 - 8 r (x Cos[t] + y Sin[t]))^3)

In[39]:=

Out[39]=

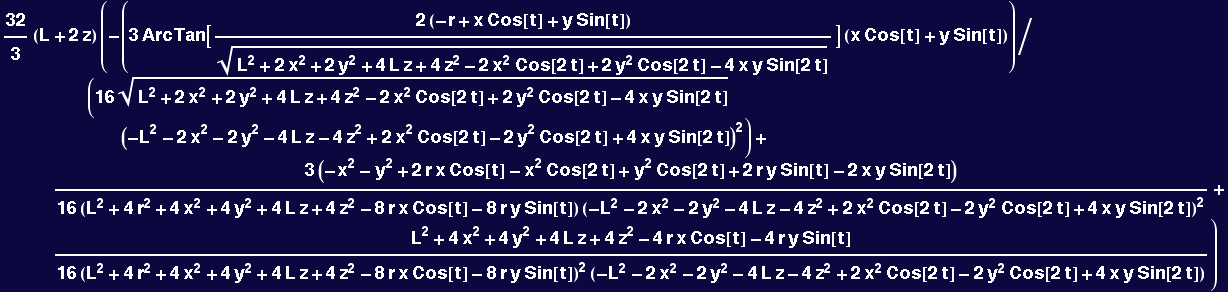
In[40]:=

$BotIntegrandθ[x_, y_, z_, CylRad_, CylLen_] := Evaluate[Simplify[(BotIntegrandθIndr/.{r->CylRad, L->CylLen}) - (BotIntegrandθIndr/.{r->0, L->CylLen})]]$

$General :: spell1 : Possible spelling error: new symbol name \"BotIntegrandθ\" is similar to existing symbol \"BotIntegrandθr\". More…$

In[41]:=

$BotContribution[xpos_, ypos_, zpos_, CylRad_ , CylLen_] := NIntegrate[Evaluate[BotIntegrandθ[xpos, ypos, zpos, CylRad, CylLen], {t, 0, 2 π}]]$

In[42]:=

$BotContribution[dist_, zpos_, CylRad_ , CylLen_] := NIntegrate[Evaluate[BotIntegrandθ[dist, 0, zpos, CylRad, CylLen], {t, 0, 2 π}]]$

In[43]:=

Out[43]=

In[44]:=

Out[44]=

Adding up all the surface integral contributions

In[45]:=

In[46]:=

Out[46]=

In[47]:=

Out[47]=

In[48]:=

In[49]:=

Visualize result as a function of radial distance at different altitudes

In[60]:=

[Graphics:HTMLFiles/Lecture-16_124.gif]

Out[60]=

The plot above shows the London potential vs. radial distance for four different z values, z = 0, z = 2/3, z = 4/3, and z= 2. The cylinder height is 4/3 and its radius is 1; for values of z that intersect the cylinder, the potential diverges as dist -> 1.

In[61]:=

[Graphics:HTMLFiles/Lecture-16_127.gif]

Out[61]=

The plot above shows the London potential vs radial distance for the same z values as in the previous plot, but for a much smaller range of potential values (-1, 0), to show the z dependence of the potential more clearly.

Visualize potential at fixed altitudes above cylinder

In[52]:=

[Graphics:HTMLFiles/Lecture-16_130.gif]

Out[52]=

The plot above shows the London potential vs. radial distance for z values equal to and larger than the cylinder height. The cylinder height is 1 and its radius is 1;.the potential is plotted for z = 1.1, z = 1.2, z = 1.3, and z= 1.4. All these z values are beyond the end of the cylinder, and the potentials do not diverge at dist = 1. Note that unlike the previous plots, this one extends from dist = 0 to 3.

The contour plot below would take an enormously long time to compute if we had not employed all of the ``integral tricks''

In[57]:=

[Graphics:HTMLFiles/Lecture-16_133.gif]

Out[57]=

Created by Mathematica (October 31, 2005)