Lecture 15 MIT 3.016 (Fall 2005) © W. Craig Carter 2003-2005

Generalizations of the Fundamental Theorem of Calculus (Part I)

Using Green's theorem in the plane to make the integration of the triangular charged surface patch simpler:

Suppose there is a uniformly charged surface (σ≡charge/area=1) occupying an equilaterial triangle in the z=0 plane:
[Graphics:HTMLFiles/Lecture-15_1.gif]

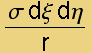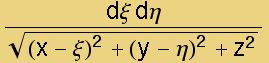
The electrical potential goes like , therefore the potential of a unit charge located at (x,y,z) from a small surface patch at (ξ,η,0) is (σ dξ dη)/r = (dξ dη)/((x - ξ)^2 + (y - η)^2 + z^2 )^(1/2)

In[1]:=

Try to convert the integral over the region to an integral over its boundary. We may be able to find a closed form—and even if not the numerical integration should be much more efficient...

We will use Green's Theorem in the Plane:
∫∫(-)dxdy = ∫(dx + dy)

Find a function, that when we take the derivative with respect to x, we get 1/r.
We will let be the function we find, and set =0

The boundary defined by the upper right side of the triangle is (ξ (t) = (1 - t)/2, η (t) = (3 ^(1/2) t)/2) ; (0 < t < 1)

To use Green's theorem in the plane ∫( -) dxdy = dx + dy
Try to find a vector function (, ) that matches the integrand over the domain. Let = 0, then to find which when differentiated by η gives 1/r

In[2]:=

F1[x_, y_ , z_] = -Integrate[1/((x - ξ)^2 + (y - η)^2 + z^2)^(1/2), η]

Out[2]=

The third (horizontal) boundary of the triangle patch looks like the easiest, let's see if an integral can be found over that patch:

In[3]:=

Out[3]=

Log[y + (1/4 + t^2 + x + x^2 - t (1 + 2 x) + y^2 + z^2)^(1/2)]

In[4]:=

Out[4]=

In[5]:=

$NEside = F1[x, y, z]/.{ξ→ (1 - t)/2, η→ (3^(1/2) t)/2}//Simplify$

Out[5]=

Log[-(3^(1/2) t)/2 + y + (1/4 + t^2 - x + x^2 + y^2 + t (-1/2 + x - 3^(1/2) y) + z^2)^(1/2)]

In[6]:=

$NWside = F1[x, y, z]/.{ξ→ -t/2, η→ (3^(1/2) (1 - t))/2}//Simplify$

$General :: spell1 : Possible spelling error: new symbol name \"NWside\" is similar to existing symbol \"NEside\". More…$

Out[6]=

Log[1/2 3^(1/2) (-1 + t) + y + (t^2/4 + t x + x^2 + (1/2 3^(1/2) (-1 + t) + y)^2 + z^2)^(1/2)]

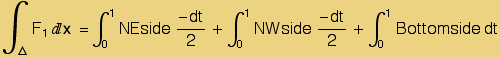
∫_△ F_1x = ∫_0^1 NEside -dt/2 + ∫_0^1 NWside -dt/2 + ∫_0^1 Bottomside dt

In[7]:=

Out[7]=

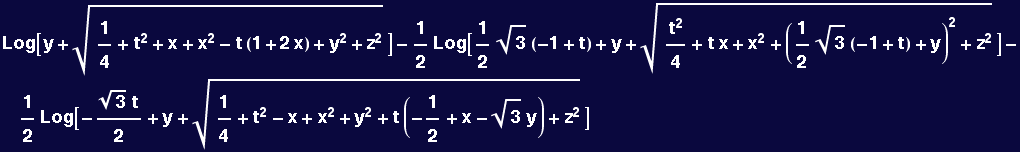
The following attempt to find a closed-form integral seems to take "forever" to evaluate and I ended up aborting it, then continuing to evaluate the remainder of the notebook.

Doing the same integral numerically

In[8]:=

$Pot[X_, Y_, Z_] := NIntegrate[Evaluate[integrand/.{x→X, y→Y, z→Z}], {t, 0, 1}]$

In[9]:=

[Graphics:HTMLFiles/Lecture-15_42.gif]

Out[9]=

Surfaces

Now we look at several different ways in which surfaces can be represented algebraically...

Surface of the form: (z=f(x,y))

In[10]:=

GraphFunction[x_, y_] := ((x - y) (x + y))/(1 + (x + y)^2)

In[11]:=

[Graphics:HTMLFiles/Lecture-15_46.gif]

Out[11]=

Surface of the form: (x(u,v), y(u,v), z(u,v))

In[12]:=

$SurfaceParametric[u_, v_] := {Cos[u] v, u Cos[u + v], Cos[u]}$

In[13]:=

[Graphics:HTMLFiles/Lecture-15_50.gif]

Out[13]=

Here is a view of the same function from a different perspective...

In[14]:=

[Graphics:HTMLFiles/Lecture-15_53.gif]

Out[14]=

The next statement plots the same parametric function over a somewhat larger range of u and v, using a clever strategy that gradually builds up the surface and serves to aid visualization of itss complex shape. After computing the sequence of plots, select them and close the group, then animate the collection.

In[15]:=

Out[15]=

Surface of the form: (F(x,y,z) = constant)

In[16]:=

In[17]:=

Out[17]=

In[18]:=

[Graphics:HTMLFiles/Lecture-15_96.gif]

Out[18]=

The following statements produce contour plots of the same function, using two different methods for colorizing the surfaces...

In[19]:=

$cpa = ContourPlot3D[x^2 - 4 x y + y^2 + y x z^2, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, Contours→ {0, 2, 8}, PlotPoints→ {5, 7}, DisplayFunction→Identity]$

Out[19]=

In[20]:=

Out[20]=

In[21]:=

[Graphics:HTMLFiles/Lecture-15_103.gif]

Out[21]=

In[22]:=

$Table[ContourPlot3D[x^2 - 4 x y + y^2 + y x z^2, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, Contours-> {i}, PlotPoints→ {5, 7}], {i, -2, 10, .5}]$

Out[22]=

Surface Integration

Example: Integrating an Orientation-Dependent Surface Tension over the surface of a cube and a sphere

Vector function for surface of sphere of radius R, u is longitude (u ∈ (0, 2π)) and v is latitude (v ∈ (-, ))

(Note: this is the parametric form of the equation of the sphere ++=.)

In[23]:=

$spheresurf[u_ , v_ ] := R {Cos[v] Cos[u] , Cos[v] Sin[u] , Sin[v]}$

The coordinate vectors at (u,v)

(Note: these vectors are tangent to the sphere surface at the point (u,v).)

In[24]:=

Out[24]=

Out[25]=

In[26]:=

The normal vector:

In[27]:=

Out[27]=

${R^2 Cos[u] Cos[v]^2, R^2 Cos[v]^2 Sin[u], R^2 Cos[v] Sin[v]}$

In[28]:=

Out[28]=

The Unit Normal: No surprise here, it is just the vector from the origin to a point on a unit sphere...

In[29]:=

Out[29]=

Now, suppose the surface energy ( ) depends on the local orientation of the surface. This is case for many single crystals. If the single crystal is cubic, it is often the case that the (100) planes have lower energy than the (111) planes. The following model for orientation-dependent surface tension has this behavior and can be employed for illustrative purposes:

In[30]:=

$General :: spell1 : Possible spelling error: new symbol name \"gamma\" is similar to existing symbol \"Gamma\". More…$

In[31]:=

Here is a plot of our model aniostropic surface energy-- the lobes at [111] indicate that those orientations have higher energy:

In[32]:=

$SphericalPlot3D[SurfaceTension[UnitNormal[u, v]]/.gamma_111 → 12, {u, 0, 2Pi}, {v, -Pi/2, Pi/2}]$

[Graphics:HTMLFiles/Lecture-15_156.gif]

Out[32]=

The total energy of a spherical particle of unit radius having the anisotropic surface tension represented above is given by the double integral

In[33]:=

Out[33]=

4/105 π (105 + gamma_111)

Compare to Cube of same volume as the unit sphere: =

In[34]:=

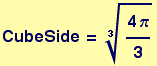
CubeSide = (4 π)/3^(1/3)

Out[34]=

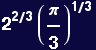
2^(2/3) (π/3)^(1/3)

In[35]:=

$CubeEnergy = 6 ( CubeSide^2 SurfaceTension[{1, 0, 0}])$

Out[35]=

In[36]:=

Out[36]=

${gamma_111→ -(105 (-6^(1/3) + π^(1/3)))/π^(1/3)}$

If the anisotropy factor is greater than about 25, then a cube is much lower energy

In[37]:=

Out[37]=

This computation compared two fixed shapes of the same volume. To find which shape of all the possible shapes, one would use a procedure known as the Wulff construction.

Created by Mathematica (October 20, 2005)