Divergence and Curl and Their Geometric Interpretations
Setting up the combined potential due to three point potentials as an example to visualize gradients, divergences, and curls
In[48]:=
![]()
A field source located a distance 1 south of the origin
In[49]:=
![]()
Sources located distance 1 at 30° and 150°:
In[50]:=
![]()
In[51]:=
![]()
Function that returns the two dimensional (x,y) gradient field of any function declared a function of two arguments:
In[52]:=
Generalizing the function to any arguments:
In[53]:=
![]()
The sum of three potentials:
In[54]:=
![]()
f(x,y) visualization of the scalar potential:
In[55]:=
![[Graphics:HTMLFiles/Lecture-13_10.gif]](HTMLFiles/Lecture-13_10.gif)
Out[55]=
![]()
Contour visualization of the three-hole potential
In[56]:=
![[Graphics:HTMLFiles/Lecture-13_13.gif]](HTMLFiles/Lecture-13_13.gif)
Out[56]=
![]()
Gradient field of three-hole potential
In[57]:=
![]()
Out[57]=
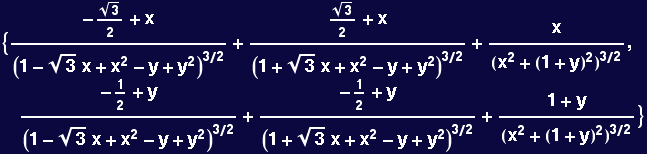
In[58]:=
![]()
In[59]:=
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-13_23.gif]](HTMLFiles/Lecture-13_23.gif)
Out[59]=
![]()
Function that takes a two-dimensional vector function of (x,y) as an argument and returns its divergence
In[60]:=
In[61]:=
![]()
Out[61]=
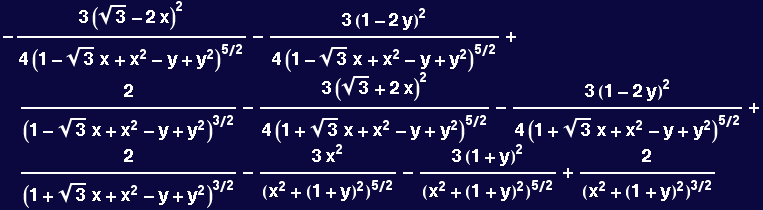
In[88]:=
![[Graphics:HTMLFiles/Lecture-13_30.gif]](HTMLFiles/Lecture-13_30.gif)
Out[88]=
![]()
It is no surprise that many of these differential operations already exist in Mathematica packages.
Using the Vector Analysis Package
In[1]:=
Coordinate Systems
Converting between coordinate systems
The spherical coordinates expressed in terms of the cartesian x,y,z
In[2]:=
![]()
Out[2]=
![{(x^2 + y^2 + z^2)^(1/2), ArcCos[z/(x^2 + y^2 + z^2)^(1/2)], ArcTan[x, y]}](HTMLFiles/Lecture-13_35.gif)
The cartesian coordinates expressed in terms of the spherical r θ φ
In[3]:=
Out[3]=
![]()
The equation of a line through the origin in spherical coodinates
In[4]:=
![]()
Out[4]=
![{(a^2 + b^2 + c^2)^(1/2) Abs[t], ArcCos[(c t)/((a^2 + b^2 + c^2)^(1/2) Abs[t])], ArcTan[a t, b t]}](HTMLFiles/Lecture-13_39.gif)
An example of calculating the positions of cities in cartesian and spherical coordinates.
In[5]:=
Boston is located at latitude 42° 21' 30" N and longitude -71°,-3',-37" W
In[6]:=
Out[6]=
![]()
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
In[15]:=
![]()
Out[15]=
![]()
In[9]:=
In[10]:=
![]()
Out[10]=
![]()
In[11]:=
![]()
In[12]:=
![]()
Out[12]=
![]()
Minimum travel distance between Boston and Paris for a round earth
In[109]:=
![]()
Out[109]=
![]()
In[110]:=
![]()
Out[110]=
![]()
In[67]:=
![SimplePot[x_ , y_ , z_, n_] := 1/(x^2 + y^2 + z^2)^n/2](HTMLFiles/Lecture-13_58.gif)
In[68]:=
Out[68]=
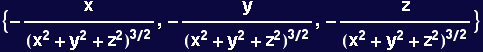
![The above is equal to Overscript[r, →]/(|| Overscript[r, →] ||)^3](HTMLFiles/Lecture-13_61.gif)
In[91]:=
![]()
In[70]:=
Out[70]=
![]()
![The above is equal to (n (n - 1) Overscript[r, →])/(|| Overscript[r, →] ||)^(2 + n)](HTMLFiles/Lecture-13_65.gif)
In[71]:=
![]()
Out[71]=
![]()

An example of Curl
There is a very useful free software tool for solving minimal surface (and many other) variational problems called Surface Evolver by Ken Brakke. To use Surface Evolver to greatest possible advantage, a user should be adept at using results from vector analysis. Mathematica's Vector Analysis package is very helpful aid for developing powerful Evolver codes. The following example is extracted from the Surface Evolver manual.
In[72]:=
![LeavingKansas[x_, y_, z_ , n_] := z^n/((x^2 + y^2) (x^2 + y^2 + z^2)^n/2) {y, -x, 0}](HTMLFiles/Lecture-13_69.gif)
In[73]:=
![]()
Out[73]=
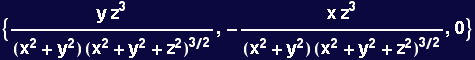
In[74]:=
![]()
Visualize the vector field for n=3, note that the function will be singular near the z-axis
In[75]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-13_82.gif]](HTMLFiles/Lecture-13_82.gif)
Out[75]=
![]()
We could make the function better behaved along the z-axis by brute force:
In[76]:=
In[77]:=
![]()
![[Graphics:HTMLFiles/Lecture-13_86.gif]](HTMLFiles/Lecture-13_86.gif)
Out[77]=
![]()
Or simply by avoiding the axis altogether and using the symmetry of the field
In[78]:=
![]()
![[Graphics:HTMLFiles/Lecture-13_89.gif]](HTMLFiles/Lecture-13_89.gif)
Out[78]=
![]()
Calculate the curl of the function using the VectorAnalysis package--note that the coordinate system is specified as cartesian.
For the particular case of n=3:
In[79]:=
Out[79]=
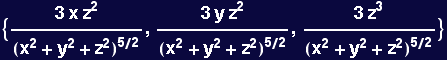
Define a new vector function for the curl for general n
In[80]:=
![]()
In[81]:=
Demonstrate the assertion that the curl has a fairly simple form and is sphericaly symmetric for n=1
In[82]:=
![]()
Out[82]=
![]()
In[83]:=
![]()
Out[83]=
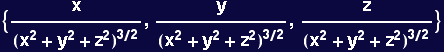
![]()
Visualize the curl for n=3
In[84]:=
![]()
![[Graphics:HTMLFiles/Lecture-13_100.gif]](HTMLFiles/Lecture-13_100.gif)
Out[84]=
![]()
Demonstrate that the divergence of the curl vanishes for the above function independent of n
In[85]:=
![]()
Out[85]=
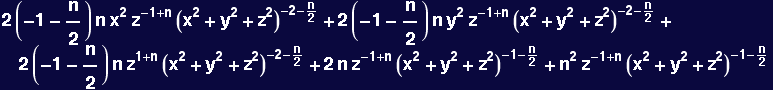
In[86]:=
![]()
Out[86]=
![]()
| Created by Mathematica (October 16, 2005) |