Lecture 12 MIT 3.016 (Fall 2005) © W. Craig Carter 2003-2005

Differential Properties of Curves

Two examples of closed curves:

Here are two vectors with components given in terms of the parameter t:

In[68]:=

$PrettyFlower[t_] := (1/4 + 3/4Cos[3t]) { Cos[t]^3, Sin[t]^3, Sin[t] Cos[t]^2}$

Both of these functions define a list of 3 positions along each axis in terms of a single parameter

In[69]:=

$Bendy[t_ ] := { Cos[t], Sin[t], Sin[t] Cos[t]}$

Defining Functions to Display Them

In[70]:=

In[71]:=

$showline[VecFunc_ , tl_ ] := Graphics3D[{Thickness[0.01], Hue[1], Line[{{0, 0, 0}, VecFunc[tl]}]}]$

In[72]:=

$showcurveline[VecFunc_ , tl_ ] := Show[{showcurve[VecFunc, tl], showline[VecFunc, tl]}, DisplayFunction→$DisplayFunction]$

In[73]:=

$CurveLineSequence[VecFunc_ ] := Table[showcurveline[VecFunc, i], {i, .1, 3 Pi, .1}]$

Animating the Curves with Their Parameter

The following command produces a sequence of 3D graphics objects that can be animated. To animate: Select all the graphics objects that are output; use the "Cell" menu to access "Cell Grouping" and select "Open/Close Group" (this will collapse the output to a single plot and make your notebook less cluttered); then use the "Cell" menu again and select "Animate Selected Graphics."

In[74]:=

Do the same thing for a different parameterized vector function:

In[75]:=

Calculating Arc Length and Re-parameterizing

Here is a general way to take a function of a general parameter, t, and compute the arc length traversed as t varies from one value to another:

In[76]:=

Out[76]=

This is the arclength up to the parameter t

In[77]:=

$General :: spell1 : Possible spelling error: new symbol name \"sFlower\" is similar to existing symbol \"Flower\". More…$

Out[77]=

Applying this to the function Bendy defined above:

In[78]:=

Out[78]=

${-Sin[t], Cos[t], Cos[t]^2 - Sin[t]^2}$

In[79]:=

$General :: spell1 : Possible spelling error: new symbol name \"sBendy\" is similar to existing symbol \"Bendy\". More…$

Out[79]=

EllipticE[2 t, 1/2]/2^(1/2)

The arc length in this case is given by a tabulated function called an elliptic integral and after checking its behavior at t = 0 we can plot it over the range {t,0,2π}:

In[80]:=

Out[80]=

In[81]:=

[Graphics:HTMLFiles/Lecture-12_213.gif]

Out[81]=

Alternatively, we can evaluate the expression for arc length numberically using the following:

In[82]:=

[Graphics:HTMLFiles/Lecture-12_217.gif]

Out[82]=

In[83]:=

$FlowerPot[u_, v_] := {(3 + Cos[v]) Cos[u], Sin[u] + (3 + Cos[v]) Sin[u], (3/2 + Cos[u + v]) Sin[v]}$

Example of a parameritized surface

In[84]:=

In[85]:=

[Graphics:HTMLFiles/Lecture-12_222.gif]

Out[85]=

A Curve on a parameritized surface

In[86]:=

[Graphics:HTMLFiles/Lecture-12_226.gif]

Out[87]=

In the above, I want to put the vine outside the surface so I scale it out a little bit...

Out[53]=

In[88]:=

[Graphics:HTMLFiles/Lecture-12_230.gif]

Out[88]=

In[89]:=

[Graphics:HTMLFiles/Lecture-12_233.gif]

Out[89]=

In[90]:=

[Graphics:HTMLFiles/Lecture-12_236.gif]

Out[90]=

Multivariable Calculus: Mathematica Review

AScalarFunction is defined everywhere in (x,y,z)

In[91]:=

In[92]:=

Out[92]=

The following lines print and they define expressions.

In[93]:=

Out[93]=

$General :: spell1 : Possible spelling error: new symbol name \"dFuncY\" is similar to existing symbol \"dFuncX\". More…$

Out[94]=

$General :: spell : Possible spelling error: new symbol name \"dFuncZ\" is similar to existing symbols {dFuncX, dFuncY} . More…$

Out[95]=

In the output lines above, partial derivatives are denoted by superscripts: e.g., (1,0,0) indicates the first partial derivative with respect to the first variable, x. The second partial with respect to y and z would be denoted by a superscript (0,1,1).

x(w,v), y(w,v), z(w,v) is a restriction of all space to a surface parameterized by (w,v),
AScalarFunction is now defined on the surface as a function of (w,v)

In[96]:=

Out[96]=

Because it is now a function of w and v, the derivative with respect to x will vanish:

In[97]:=

Out[97]=

Two more flavors of derivatives, these are partial derivatives evaluated on the surface

In[98]:=

$General :: spell : Possible spelling error: new symbol name \"dFuncW\" is similar to existing symbols {dFuncX, dFuncY, dFuncZ} . More…$

Out[98]=

In[99]:=

$General :: spell : Possible spelling error: new symbol name \"dFuncV\" is similar to existing symbols {dFuncW, dFuncX, dFuncY, dFuncZ} . More…$

Out[99]=

On the surface x(w,v), y(w,v), z(w,v), we can prescribe a curve w(t), v(t), now we have
AScalarFunction defined on that curve

In[100]:=

Out[100]=

The following is a derivative of the function along the curve parameterized by t

In[101]:=

$General :: spell : Possible spelling error: new symbol name \"dFuncT\" is similar to existing symbols {dFuncV, dFuncW, dFuncX, dFuncY, dFuncZ} . More…$

Out[101]=

Note on the step immediately above: by specifying w and v, values of x and y are specified, and additionally values of z. The three functions x(w,v), y(w,v), and z(w,v) together describe a surface---it specifies that three points can be specified by two values (A familiar case is when w=x, and v=y, then z(x,y) is a surface that can be specified over the x-y plane. The functions w(t) and v(t) trace out a plane curve on the w-v surface and map onto a corresponding twisted curve (see Kreyszig p.429 for distinction between "plane" and "twisted" if it is not obvious).

Finally, we could skip the surface and just define a space curve x(t), y(t), z(t) and take the derivative of AScalarFunc along that curve:

In[102]:=

Out[102]=

Visualizing approximations (Taylor Expansions) to surfaces at points

Getting Mathematica to represent a general change in a function--multidimensional versions of Taylor expansions

In[103]:=

Out[103]=

In[104]:=

Out[104]=

The next step eliminates second- and third-order terms… (remember, dx, dy, and dz are small)

In[105]:=

Out[105]=

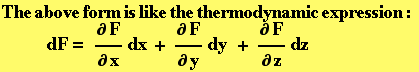
The above form is like the thermodynamic expression : dF = ∂F/∂xdx + ∂F/∂ydy + ∂F/∂zdz

Example of using Taylor Expansion to turn a function of two variables into an approximating function of four variables:

In[106]:=

CrazyFun[x_, y_] := (Sin[5π x] Sin[5π y] )/(x y) + ( Sin[5π (x - 1)] Sin[5π (y - 1)])/((x - 1) ( y - 1))

Plot this function over suitable range of the variables x and y:

In[107]:=

[Graphics:HTMLFiles/Lecture-12_280.gif]

Out[107]=

Now, approximate the function about a specific point (xo, yo), using Mathematica's Series function:

In[108]:=

$Approxfunction[x_, y_ , xo_ , yo_] := Series[CrazyFun[x, y], {x, xo, 2}, {y, yo, 2}]//Normal$

and plot the approximate function in the neighborhood of (xo, yo):

In[109]:=

[Graphics:HTMLFiles/Lecture-12_284.gif]

Out[109]=

Both the original and the approximate function can be plotted simultaneously:

In[110]:=

[Graphics:HTMLFiles/Lecture-12_287.gif]

Out[110]=

This final little bit selects random points (xo, yo) and fits Taylor expansions to ten different points, then displays them individually as well as with a superposed plot of the original function.

In[111]:=

The next function automates the small approximating surface patch

In[112]:=

To build a sequence of graphics, I'll build a stack of ten graphics objects by using a recursive method. The next command sets the end of the recursion loop.

In[113]:=

In[114]:=