Time Dependent Solution to the Diffusion Equation in thePlane with a source at the origin.
Note: This notebook will produce some neat animations but they each take some time to compute. And, if you save the notebook with the graphics, it will require 50MB or so of hard disk space.
You should definitely take the time to learn how to make your own animations because the results can be really instructive. You can even save animations in various formats and then import them in separate applications.
![]()
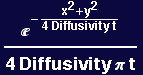
Let the diffusivity be 1 for visualization purposes
![]()
![]()
![]()
Flux is a vector that points in the direction of the flow and is a measure of how much is flowing per unit time
![]()
![]()
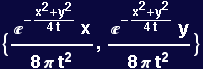
![]()
![[Graphics:HTMLFiles/Lecture-11_198.gif]](HTMLFiles/Lecture-11_198.gif)
![]()
![]()
![[Graphics:HTMLFiles/Lecture-11_201.gif]](HTMLFiles/Lecture-11_201.gif)
![]()
To see animations,use the menu command to group all the graphics cells together, and then animate

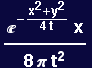
To see animations,use the menu command to group all the graphics cells together, and then animate
![]()
To see animations,use the menu command to group all the graphics cells together, and then animate
![]()
![]()
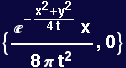
To see animations,use the menu command to group all the graphics cells together, and then animate
![]()

Cross products:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Derivatives of Vectors
![]()
![]()
![[Graphics:HTMLFiles/Lecture-11_731.gif]](HTMLFiles/Lecture-11_731.gif)
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-11_736.gif]](HTMLFiles/Lecture-11_736.gif)
![]()
![]()
![[Graphics:HTMLFiles/Lecture-11_739.gif]](HTMLFiles/Lecture-11_739.gif)
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-11_744.gif]](HTMLFiles/Lecture-11_744.gif)
![]()
![]()
![[Graphics:HTMLFiles/Lecture-11_747.gif]](HTMLFiles/Lecture-11_747.gif)
![]()
![]()
![]()
To see animations,use the menu command to group all the graphics cells together, and then animate
| Created by Mathematica (October 12, 2005) |