Stress Strain, Principal Axes, and Mohr's Circle

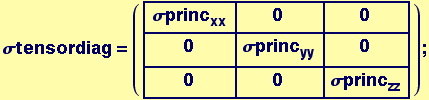
General Stress State  in Principal Axes  System

This is a general state, we will rotate about the z-axis and compare the result to a general two-dimensional stress state.

σtensordiag = ({{σprinc_xx, 0, 0}, {0, σprinc_yy, 0}, {0, 0, σprinc_zz}}) ;

σtensordiag//MatrixForm

( {{σprinc_xx, 0, 0}, {0, σprinc_yy, 0}, {0, 0, σprinc_zz}} )

Rotation about z-axis by angle θ

rotmat[θ_] := ({{Cos[θ], -Sin[θ], 0}, {Sin[θ], Cos[θ], 0}, {0, 0, 1}}) ;

rotmat[θ]//MatrixForm

( {{Cos[θ], -Sin[θ], 0}, {Sin[θ], Cos[θ], 0}, {0, 0, 1}} )

Transformation to general two-dimensional stress state coordinate system by rotating the principal system by θ around z-axis

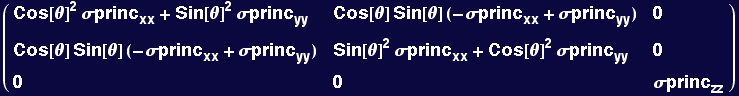
σrot = Simplify[Transpose[rotmat[θ]] . σtensordiag . rotmat[θ]] ;

σrot//MatrixForm

Writing the same equation in a slightly different way...

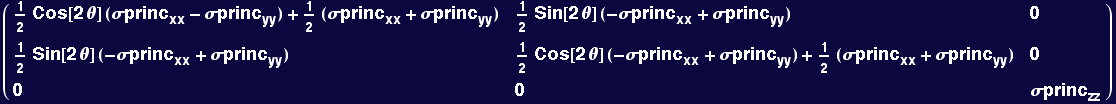
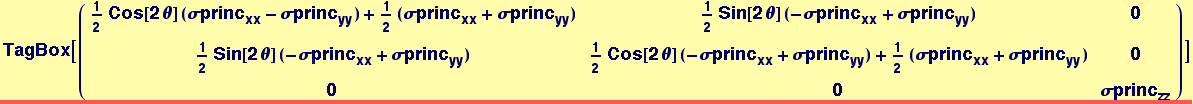
σrotalt = Collect[σrot//TrigReduce, {Cos[2θ], Sin[2 θ]}] ;

σrotalt//MatrixForm

Naming the coefficients of the two-dimensional state in the rotated principal system

( {{σlab_xx, σlab_xy, σlab_xz}, {σlab_xy, σlab_yy, σlab_yz}, {σlab_xz, σlab_yz, σlab_zz}} ) = σrotalt ;

1. σlab_xx  in laboratory system rotated by θ from principal axis system

σlab_xx

1/2 Cos[2 θ] (σprinc_xx - σprinc_yy) + 1/2 (σprinc_xx + σprinc_yy)

1/2 Cos[2 θ] (σprinc_xx - σprinc_yy) + 1/2 (σprinc_xx + σprinc_yy)

2. σlab_yy  in laboratory system rotated by θ from principal axis system

σlab_yy

1/2 Cos[2 θ] (-σprinc_xx + σprinc_yy) + 1/2 (σprinc_xx + σprinc_yy)

1/2 Cos[2 θ] (-σprinc_xx + σprinc_yy) + 1/2 (σprinc_xx + σprinc_yy)

3. σlab_xy  in laboratory system rotated by θ from principal axis system

σlab_xy

1/2 Sin[2 θ] (-σprinc_xx + σprinc_yy)

1/2 Sin[2 θ] (-σprinc_xx + σprinc_yy)

All z - components remain zero except the original diagonal term σlab_zz :

σlab_yz

σlab_xz

σlab_zz

0

0

0

0

σprinc_zz

σprinc_zz

Equations 1, 2, and 3 are the equations that express a circle known as Mohr's circle of stress (see accompanying class notes). The equations show the way in which the stress tensor components in a two-dimensional state of stress (a "biaxial" stress state) vary with orientation of the coordinate system in which the stresses are described.

Notice that there are two invariants of the general stress :

The trace (or twice the offset of Mohr's Circle):

Simplify[σlab_xx + σlab_yy ]

σprinc_xx + σprinc_yy

σprinc_xx + σprinc_yy

And the determinant

Simplify[σlab_xx  σlab_yy - (σlab_xy)^2]

σprinc_xx σprinc_yy

σprinc_xx σprinc_yy

These last two results are precisely the trace and determinant of the x and y terms in the original diagonal form of the stress state, thus illustrating the invariance of these quantities under rotation of coordinate rotations.

Example of Mohr's circle for two-dimensional body in uniaxial tension with σprinc_xx = 10 MPa and all other stress components equal to zero

σprinc_xx = 10. ;

σprinc_yy = 0. ;

σprinc_xy = 0. ;

[Graphics:HTMLFiles/Lecture-10_50.gif]

-Graphics -

-Graphics -

Comparing this plot with Figure 10-3 in the lecture notes, we see that the maximum and minimum tensile stresses are 10 and 0 MPa (from intercepts with x axis), as expected, and the maximum shear stress is ±5 MPa and it is experienced on a plane oriented at 2θ = 90° or θ = 45° to the tensile axis (remember that angles on Mohr's circle plots are twice the angle in the body).

Created by Mathematica  (October 5, 2005) Valid XHTML 1.1!