Vectors and Matrices

In[1]:=

Out[1]=

Out[2]//MatrixForm=

In[3]:=

Out[4]//MatrixForm=

In[5]:=

Out[5]=

The matrix multiplication does not work because the sizes are inconsistent.

In[6]:=

In[7]:=

Out[8]//MatrixForm=

In[9]:=

Out[10]//MatrixForm=

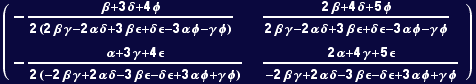
In[11]:=

Out[11]=

In[12]:=

Out[12]//MatrixForm=

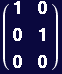
Same example for water and water complexes: use the matrix watmat to store molecular formulas for each type of molecule in the system

In[13]:=

Out[14]//MatrixForm=

The vector molvec is used to store the number of each kind of molecule

In[15]:=

Out[15]=

The vector atomvec is used to store the number of each atomic species that is present

In[16]:=

Out[16]=

In[17]:=

Out[17]//MatrixForm=

The vector eq is now defined and its two elements are equations that give the number of hydrogen atoms and the number of oxygen atoms:

In[18]:=

Out[18]=

In[19]:=

Out[19]=

In[20]:=

In[21]:=

Out[21]=

Created by Mathematica  (September 21, 2005)