Lecture 04 MIT 3.016 (Fall 2005) © W. Craig Carter 2003-2005

Symbolic and Numeric Calculations, Roots Finding,
File Input and Output

Mathematica has a powerful array of functions that solve equations symbolically and ways to simplify expressions. Many people use Mathematica because it removes the tedium of doing algebra with pencil and paper---and perhaps more importantly it doesn't make errors! However, one frustrating aspect is getting Mathematica to represent an expression in exactly the form you desire. Sometimes it is possible with patience,practice and skill---and sometimes you have to give up and accept that the form of the expression will not be ``neat and compact.''

Operations on Polynomials, Rational Expressions, and Simplification of Expressions

A good way to gain familiarity with Mathematica's operations to do symbolic algebra is to look though the categories in the Built-in Functions section in the Help Browser. Look though the names of functions under Algebraic Computation--they have names that are fairly indicative of their purpose.

In[3]:=

Out[3]=

In[4]:=

Out[4]=

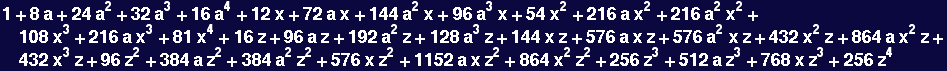
In[5]:=

Out[5]=

In[6]:=

Out[6]=

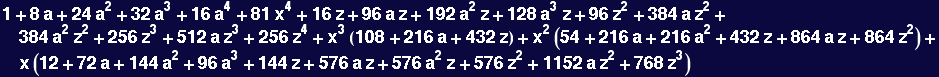
In[7]:=

Out[7]=

In[8]:=

$PaulSpiffedUp = Sum[Simplify[Coefficient[PaulinX, x, i]] x^i, {i, 0, 20}]$

Out[8]=

In[9]:=

Out[9]=

In[10]:=

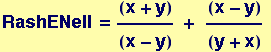
RashENell = (x + y)/(x - y) + (x - y)/(y + x)

Out[10]=

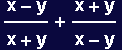
(x - y)/(x + y) + (x + y)/(x - y)

In[11]:=

Out[11]=

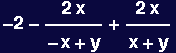
-2 - (2 x)/(-x + y) + (2 x)/(x + y)

In[12]:=

Out[12]=

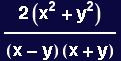
(2 (x^2 + y^2))/((x - y) (x + y))

In[13]:=

Out[13]=

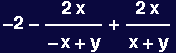
-2 - (2 x)/(-x + y) + (2 x)/(x + y)

In[14]:=

Out[14]=

In[15]:=

Out[15]=

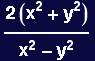
(2 (x^2 + y^2))/(x^2 - y^2)

In[16]:=

Out[16]=

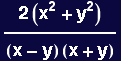
(2 (x^2 + y^2))/((x - y) (x + y))

One common hurdle is getting Mathematica to remove roots:

In[17]:=

Out[17]=

In[18]:=

Out[18]=

Note in the following statement that "x ∈ Reals" means "x is a real number" and "&&" is the "Logical And" operator.

In[19]:=

Out[19]=

In[20]:=

Out[20]=

Brute force; clever ,but not a good idea follows:

In[21]:=

Out[21]=

Calculus

In[22]:=

AMessyExpression = Log[x Sin[x]]/1/x

Out[22]=

In[23]:=

Out[23]=

In[24]:=

Out[24]=

In[25]:=

Out[25]=

In[26]:=

Out[26]=

1/2  (2 - 2   +  π - Log[4] + 2 Log[1 - ^(2  )])

In[27]:=

Out[27]=

In[28]:=

Out[28]=

In[29]:=

Out[29]=

∫Sin[x]/(a^2 + x^2)^(1/2) x

In[30]:=

Out[30]=

Integrate[Sin[x]/(a^2 + x^2)^(1/2), x, Assumptions→a≥0]

In[31]:=

Integrate[Sin[x]/(a^2 + x^2)^(1/2), x, Assumptions→Re[a^2] >0]

Out[31]=

Integrate[Sin[x]/(a^2 + x^2)^(1/2), x, Assumptions→Re[a^2] >0]

In[32]:=

$UglyInfiniteIntegral = Integrate[Sin[x]/Sqrt[(x^2 + a^2)], {x, 0, ∞}, Assumptions→Re[a^2] >0]$

Out[32]=

1/2 π (BesselI[0, a] - (a StruveL[0, a])/a^2^(1/2))

In[33]:=

Out[33]=

Now we will introduce the Taylor expansion capabilities in Mathematica:

In[34]:=

Out[34]=

2 Log[x] x - x^3/6 + O[x]^5

In[35]:=

Out[35]=

-x^3/6 + 2 x Log[x]

In[36]:=

[Graphics:HTMLFiles/Lecture-04_69.gif]

Out[36]=

Solving Equations

In[37]:=

Out[37]=

Note the use of Equal (==) rather than Set (=) in the following; using "=" will produce an error message.

In[38]:=

Out[38]=

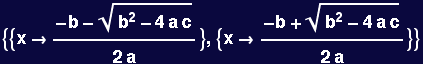
${{x→ (-b - (b^2 - 4 a c)^(1/2))/(2 a)}, {x→ (-b + (b^2 - 4 a c)^(1/2))/(2 a)}}$

Note that the roots are given as Rules. Now we ask Mathematica to verify that the solutions it found are indeed roots to the specified equation. Here is a prototypical example of using Replace (/.) to accomplish this:

In[39]:=

Out[39]=

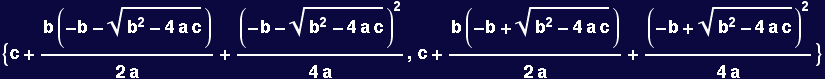
${c + (b (-b - (b^2 - 4 a c)^(1/2)))/(2 a) + (-b - (b^2 - 4 a c)^(1/2))^2/(4 a), c + (b (-b + (b^2 - 4 a c)^(1/2)))/(2 a) + (-b + (b^2 - 4 a c)^(1/2))^2/(4 a)}$

In[40]:=

Out[40]=

More examples of using Solve:

In[41]:=

In[42]:=

$TheQuinticEquation = Sum[a[i] x^i, {i, 0, 5}]$

Out[42]=

In[43]:=

Out[43]=

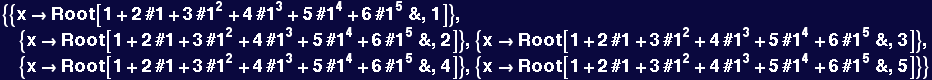
In[44]:=

Out[44]=

Out[45]=

In[46]:=

Out[46]=

Numerical Solutions

In[47]:=

Out[47]=

∫Sin[x]/(a^2 + x^2)^(1/2) x

In[48]:=

$Integrate[Sin[ x]/Sqrt[(x^2 + a^2)], {x, 0, 1}]$

Out[48]=

∫_0^1Sin[x]/(a^2 + x^2)^(1/2) x

In[49]:=

$NIntegrate[(Sin[ x]/Sqrt[(x^2 + a^2)])/.a→1, {x, 0, 2 Pi}]$

Out[49]=

In[50]:=

$Plot[NIntegrate[Sin[ x]/Sqrt[(x^2 + a^2)], {x, 0, 2 Pi}] , {a, 0, 10}]$

[Graphics:HTMLFiles/Lecture-04_97.gif]

Out[50]=

In[51]:=

[Graphics:HTMLFiles/Lecture-04_100.gif]

Out[51]=

In[52]:=

Out[52]=

In[53]:=

Out[53]=

In[54]:=

Out[54]=

In[55]:=

Out[55]=

File Input and Output

In[56]:=

In[57]:=

In[58]:=

Out[58]=

The next statement retrieves the content of Afile.m, but does not associate it with any name (in particular, with AMessyExpression!):

In[59]:=

Out[59]=

In[60]:=

Out[60]=

In[61]:=

Out[61]=

The next statement introduces the "show file" command, !!

In[62]:=

x*Log[x*Sin[x]]

In[63]:=

Out[63]=

In[64]:=

Out[64]=

In[65]:=

Out[65]=

In[66]:=

In[67]:=

In[68]:=

In[69]:=

{{0.314289, 0.438625}, {0.854381, 0.626077}, {0.169051, 0.975279},

  {0.552001, 0.338474}, {0.670668, 0.585666}, {0.252752, 0.179965},

  {0.503252, 0.932187}, {0.911903, 0.582839}, {0.775185, 0.33409},

  {0.030177, 0.444192}, {0.842548, 0.205801}, {0.981605, 0.966909},

  {0.528258, 0.767176}, {0.127223, 0.340832}, {0.359207, 0.791898},

  {0.575223, 0.00235831}, {0.68854, 0.206232}, {0.322471, 0.822394},

  {0.185288, 0.274044}, {0.410568, 0.239555}}
0.314289     0.438625

0.854381     0.626077

0.169051     0.975279

0.552001     0.338474

0.670668     0.585666

0.252752     0.179965

0.503252     0.932187

0.911903     0.582839

0.775185     0.33409

0.030177     0.444192

0.842548     0.205801

0.981605     0.966909

0.528258     0.767176

0.127223     0.340832

0.359207     0.791898

0.575223     0.00235831

0.68854      0.206232

0.322471     0.822394

0.185288     0.274044

0.410568     0.239555

In[70]:=

Out[70]=

Using Packages

Fortunately, others have gone to the trouble of writing files full of useful stuff--and you can load this stuff into Mathematica for your very own use. Some people produce useful stuff and you can buy it, which is nice if you find it valuable--and you can write stuff and gain value by selling it, which might be even more nice.
Mathematica comes with a group of Standard Packages, that you can load in to do special tasks. The Packages are listed under "Add-ons & Links" in the Help Browser. For example, take a look at the specialized package under "Miscellaneous" called "World Plot"...

In[71]:=