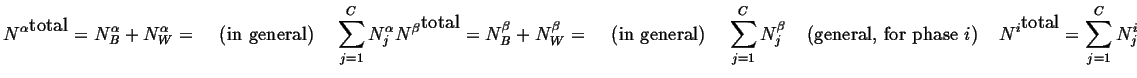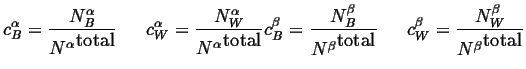

Next: An Illustrative Example
Up: Lecture_18_web
Previous: Equilibrium for Systems with
We now consider a very important system that has
internal degrees of freedom:
a system composed of variable
chemical elements and various phases.
In other words, the internal degrees of freedom
are the compositions of the various regions
that compose our system.
This topic often confuses students, so I will go
over the terms very carefully, first a few
definitions:
- phase
- A part of a system that can be indentified as
``different'' from another part of the system.
A phase is always separated from another phase by
an identifiable interface.
Examples of phases are a solution of iron and carbon
in an FCC structure and a solution of iron and carbon
in a BCC structure.
- composition
- The fractions of the various chemical components that
comprise a system.
- phase fraction of
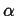
- The fraction of a system that is the
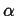 -phase.
-phase.
- composition of phase
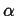
- The composition of the subsystem composed of
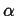 -phase
alone.
-phase
alone.
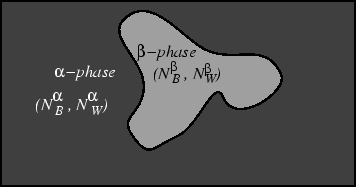
Figure 18-4:
A system
in equilibrium with its surroundings and
composed of two phases 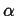 and
and 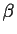 , each having
a different chemical composition.
This illustration is for two phases and two
independent components but it may be extrapolated to
to as many phases and components as required.
Later, a relation
between the number of phases
, each having
a different chemical composition.
This illustration is for two phases and two
independent components but it may be extrapolated to
to as many phases and components as required.
Later, a relation
between the number of phases 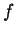 and the
number of components
and the
number of components 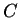 that can exist at equilibrium
will be derived.
that can exist at equilibrium
will be derived.
 |
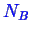 and
and
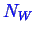 represent numbers of
represent numbers of
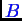 - and
- and
 type molecules.
The number of moles in phases
type molecules.
The number of moles in phases
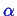 and in phase
and in phase
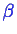 can be varied.
can be varied.
The following notation should be studied carefully.
Therefore the total numbers of
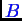 molecules (or atoms) and
molecules (or atoms) and
 molecules in the system are:
molecules in the system are:
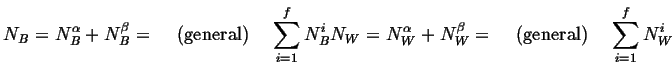 |
(18-2) |
The total number of atoms in the system is
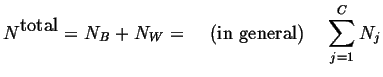 |
(18-3) |
The average composition in the system is
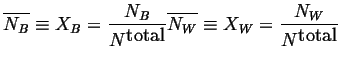 |
(18-4) |
Furthermore, we can find the total number
of atoms (molecules) in the
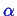 -phase:
-phase:
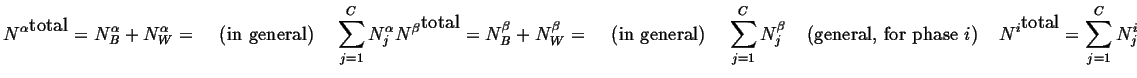 |
(18-5) |
And the compositions of the phases can be
defined as:
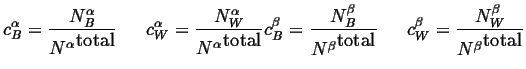 |
(18-6) |


Next: An Illustrative Example
Up: Lecture_18_web
Previous: Equilibrium for Systems with
W. Craig Carter
2002-10-20

![]() and
and
![]() represent numbers of
represent numbers of
![]() - and
- and
![]() type molecules.
The number of moles in phases
type molecules.
The number of moles in phases
![]() and in phase
and in phase
![]() can be varied.
can be varied.

![]() molecules (or atoms) and
molecules (or atoms) and
![]() molecules in the system are:
molecules in the system are:
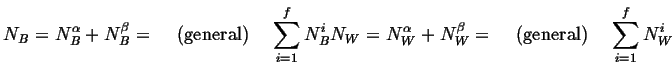
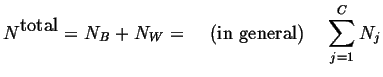
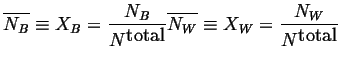
![]() -phase:
-phase: